2025-07-26

B-Tree

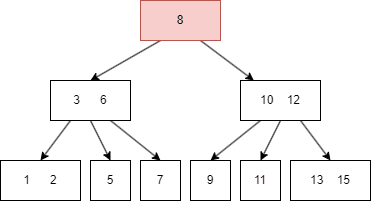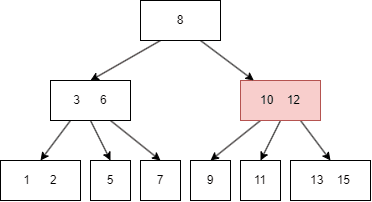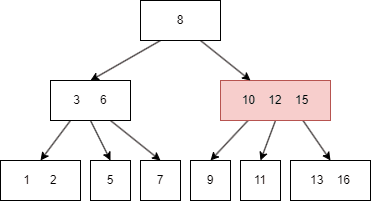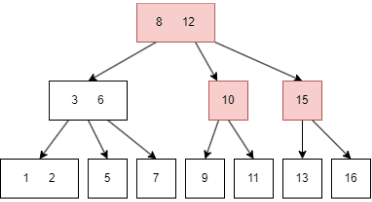
트리 형태이지만 2개 이상의 자식 노드를 가질 수 있는 트리

하나의 노드에 여러 개의 키(key) 저장 가능

부모 노드의 key값 범위가 자식 노드를 배치하는데 중요

부모 노드의 key들은 오름차순으로 정렬

B-Tree는 최소 키 한 개, 최소 노드 두 개가 필요하다

각 노드는 정렬된 키들을 여러 개 가질 수 있음
하나의 노드는 최대 2t−1개의 키, 최대 2t개의 자식을 가짐
(t는 최소 차수, 최소 t - 1개 키 보유)
모든 리프는 같은 레벨
노드가 꽉 차면 중간 키를 부모로 올리고 분할(split)

루트 노드를 제외한 모든 노드는 최소 ⌈M/2⌉ 개의 자식을 가져야 한다

M개의 자녀를 가질 수 있는 B-Tree를 M차 B-Tree라고 부른다

⌈M - 1⌉ : 각 노드의 최대 key 수

⌈M / 2⌉ : 각 노드의 최소 자녀 노드 수

⌈M / 2 - 1⌉ : 각 노드의 최소 key 수

Internal Node의 key수가 x개라면, 자녀의 노드 수는 언제나 x + 1 이다

추가는 항상 leaf 노드에 한다

노드가 넘치면 가운데 key를 기준으로 좌우 key들은 분할하고 가운데 key는 승진한다

Root Node : 트리의 가장 위에 있는 노드
Internal Node(내부 노드) : 자식 노드를 하나 이상 가지고 있는 노드
Leaf Node(자녀 노드) : 자식 노드가 없는 끝 노드

코드 리뷰

class BTreeNode:
    def __init__(self, t, leaf=False):
        self.t = t  # 최소 차수
        self.leaf = leaf
        self.keys = []       # 현재 노드의 키들
        self.children = []   # 자식 노드들

    def __str__(self, level=0):
        result = "  " * level + str(self.keys) + "\n"
        for child in self.children:
            result += child.__str__(level + 1)
        return result

class BTree:
    def __init__(self, t=2):
        self.t = t
        self.root = BTreeNode(t, leaf=True)

    def search(self, k, node=None):
        if node is None:
            node = self.root
        i = 0
        while i < len(node.keys) and k > node.keys[i]:
            i += 1
        if i < len(node.keys) and k == node.keys[i]:
            return True
        if node.leaf:
            return False
        return self.search(k, node.children[i])

    def insert(self, k):
        root = self.root
        if len(root.keys) == 2 * self.t - 1:
            new_root = BTreeNode(self.t, leaf=False)
            new_root.children.append(self.root)
            self.split_child(new_root, 0)
            self.root = new_root
        self._insert_non_full(self.root, k)

    def _insert_non_full(self, node, k):
        i = len(node.keys) - 1
        if node.leaf:
            node.keys.append(0)  # 공간 확보
            while i >= 0 and k < node.keys[i]:
                node.keys[i + 1] = node.keys[i]
                i -= 1
            node.keys[i + 1] = k
        else:
            while i >= 0 and k < node.keys[i]:
                i -= 1
            i += 1
            if len(node.children[i].keys) == 2 * self.t - 1:
                self.split_child(node, i)
                if k > node.keys[i]:
                    i += 1
            self._insert_non_full(node.children[i], k)

    def split_child(self, parent, i):
        t = self.t
        full_child = parent.children[i]
        new_child = BTreeNode(t, leaf=full_child.leaf)

        # 중간 키를 부모로 올림
        parent.keys.insert(i, full_child.keys[t - 1])
        parent.children.insert(i + 1, new_child)

        # 키/자식 분할
        new_child.keys = full_child.keys[t:]
        full_child.keys = full_child.keys[:t - 1]

        if not full_child.leaf:
            new_child.children = full_child.children[t:]
            full_child.children = full_child.children[:t]

    def print_tree(self):
        print(self.root)

# 테스트
btree = BTree(t=2)
data = [10, 20, 5, 6, 12, 30, 7, 17]

for value in data:
    btree.insert(value)

btree.print_tree()

# 검색 테스트
print("Search 6:", btree.search(6))    # True
print("Search 21:", btree.search(21))  # False

시간 복잡도

M : B-Tree의 차수 (한 노드가 가질 수 있는 최대 자식 수)
N : 트리에 저장된 전체 키의 수

연산	시간 복잡도	설명
검색 (Search)	O(logₘ N)	트리의 높이에 비례하며, logₘ N 단계만 내려가면 됨
삽입 (Insert)	O(logₘ N)	리프까지 내려간 뒤, 필요 시 분할 발생
삭제 (Delete)	O(logₘ N)	리프까지 내려간 뒤, 필요 시 병합/차용 발생