다이나믹 프로그래밍(Dynamic Programming)

 

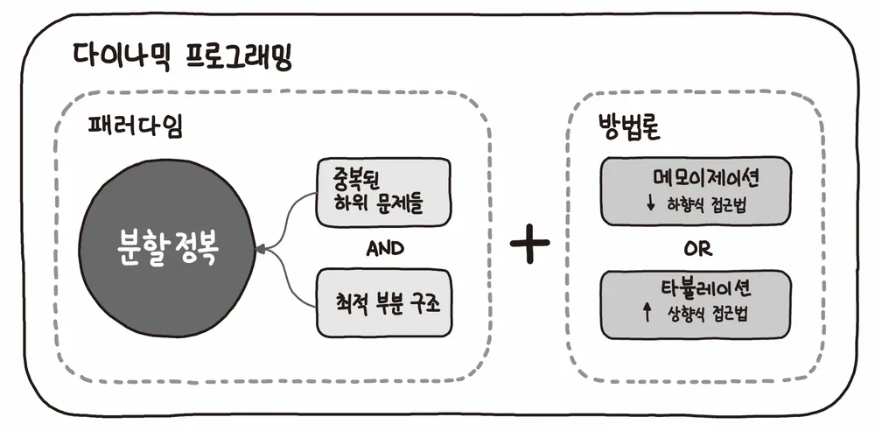
동적 계획법(DP)는 최적화 문제를 풀기 위한 사고 방식(문제 해결 전략, Paradigm)

이미 계산한 것은 다시 계산하지 말고, 저장해서 재활용하자

 

코드 리뷰

재귀 방식

피보나치 수열을 재귀로 풀면 아래처럼 똑같은 계산을 여러 번 하게 된다

def fib(n):
    if n <= 1:
        return n
    return fib(n-1) + fib(n-2)

 

재귀 기반 DP

def fib(n, memo={}):
    if n <= 1:
        return n
    if n not in memo:
        memo[n] = fib(n - 1, memo) + fib(n - 2, memo)
    return memo[n]

 

반복문 기반 DP

def fib(n):
    dp = [0] * (n + 1)
    dp[1] = 1
    for i in range(2, n + 1):
        dp[i] = dp[i - 1] + dp[i - 2]
    return dp[n]

이런 낭비를 줄이기 위해, 이미 계산한 값을 저장하고 필요할 때 꺼내쓰는 방법이 동적 계획법

 

핵심 개념

• 메모이제이션(Memoization)
  -> 필요할 때마다 계산하고 결과를 저장함, 재귀 방식, (Top-down)

• 테이블화(Tabulation)
  -> 배열이나 테이블을 사용하여 가장 작은 문제부터 차례대로 전부 계산함, 반복문 방식, (Bottom-up)

• 최적 부분 구조(Optimal Substructure)
  -> 큰 문제의 답이 작은 문제들의 답을 조합해서 만들어질 수 있음

• 중복 부분 문제(Overlapping Subproblems)
  -> 같은 계산을 여러 번 해야 하는 구조를 가지고 있음

 

탑다운 vs 바텀업

구분	메모이제이션 (Top-down)	테이블화 (Bottom-up)
구조	재귀 호출	반복문
계산 시점	호출될 때 계산	처음부터 순차적으로 계산
장점	코드가 직관적	성능이 더 안정적일 수 있음
단점	스택 오버플로우 위험	코드가 복잡할 수 있음

 

시간 복잡도

구현 방식	시간 복잡도	공간 복잡도	설명
일반 재귀 (순수 재귀)	O(2ⁿ)	O(n)	중복 계산이 많아 매우 비효율적
메모이제이션 (Top-down)	O(n)	O(n)	재귀 + 캐싱. 각 값은 한 번만 계산
테이블화 (Bottom-up)	O(n)	O(n) or O(1)*	반복문 기반. 공간 최적화 가능