2025-07-26

그래프(graph)

그래프는 정점과 간선으로 이루어진 자료구조이다

그래프-1

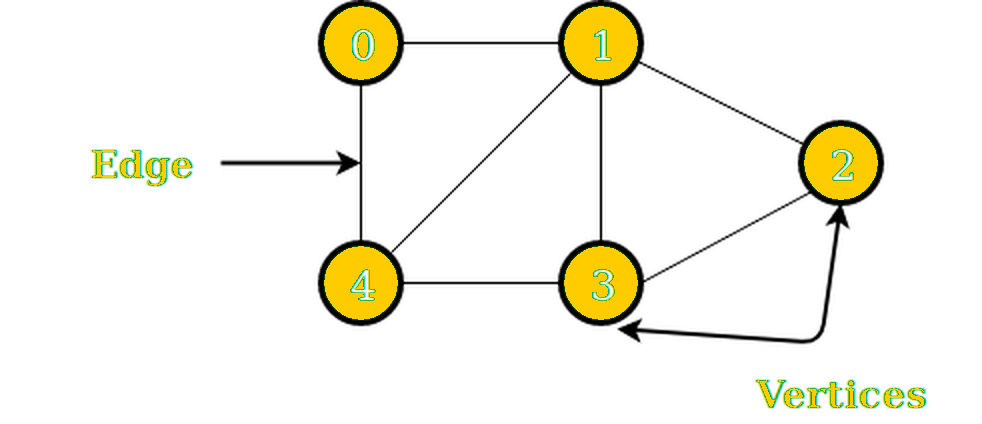
차수(degree)는 각 정점에 대해서 간선으로 연결된 이웃한 정점의 개수가 바로 차수이다

그래프의 간선에는 방향성이 있을 수 있다

방향성이 없으면 무방향 그래프라고 하고 방향성이 있다면 방향 그래프라고 한다

방향 그래프에서는 자기에게서 나가는 간선의 개수는 진출 차수(outdegree)이고 들어오는 간선의 개수는 진입 차수(indegree)이다

사이클은 한 점에서 출발해서 자기 자신으로 돌아올 수 있는 경로를 말한다

순환(Cyclic graph) 그래프는 사이클이 하나라도 있어야 한다

사이클이 없으면 비순환 그래프(Acyclic graph)라고 한다

모든 서로 다른 정점 쌍이 간선으로 연결된 그래프를 완전 그래프(Complete Graph)라고 한다

임의의 두 정점 사이 경로가 항상 존재하는 그래프는 연결 그래프(Connected Graph)라고 한다

루프는 한 정점에서 시작해서 같은 정점으로 들어오는 간선을 말한다

단순 그래프(Simple Graph)는 두 정점 사이 간선이 1개 이하이고 루프가 존재하지 않는 그래프이다

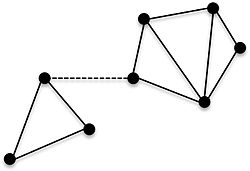완전 그래프 연결 그래프

연결 그래프 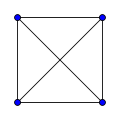완전 그래프

방향성과 그래프

무방향 그래프 (Undirected Graph) : 간선에 방향이 없음
방향 그래프 (Directed Graph) : 간선이 한 방향으로 연결됨

차수 (Degree) : 정점에 연결된 간선의 개수

무방향 그래프 : 연결된 이웃 정점의 수
방향 그래프 :
- 나가는 간선 수 → 진출 차수 (Outdegree)
- 들어오는 간선 수 → 진입 차수 (Indegree)

밀도 : 간선의 수가 정점의 수에 비해 얼마나 많은지를 나타내는 지표

희소 그래프(Sparse) - 인접 리스트(Adjacency List)
조밀 그래프(Dense) - 인접 행렬(Adjacency Matrix)

용어	설명
사이클 (Cycle)	정점들을 거쳐 다시 시작 정점으로 돌아오는 경로로, 같은 간선을 두 번 이상 사용하지 않는다
순환 그래프 (Cyclic Graph)	하나 이상의 사이클이 있는 그래프
비순환 그래프 (Acyclic Graph)	사이클이 전혀 없는 그래프
완전 그래프 (Complete Graph)	모든 정점 쌍이 간선으로 연결된 그래프
연결 그래프 (Connected Graph)	모든 정점 쌍 사이에 경로가 존재하는 그래프
루프 (Loop)	하나의 정점에서 시작해 자신에게 다시 연결된 간선
단순 그래프 (Simple Graph)	루프가 없고, 두 정점 사이 간선이 하나 이하인 그래프

그래프의 표현법

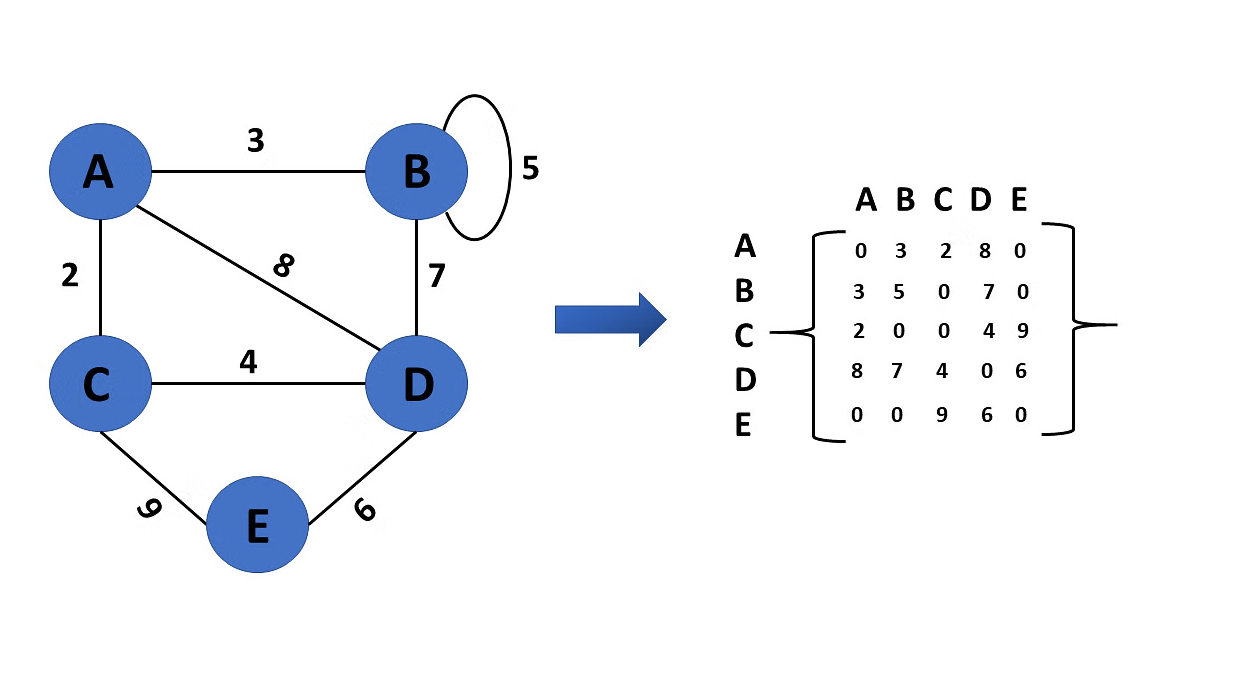
그래프와 행렬

첫 번째 방법으로는 인접 행렬을 이용한다

정점이 V개이고 간선이 E개일 때 어떤 두 점이 연결되어 있는지를 O(1)에 알 수 있다는 장점이 있다

가로와 세로가 각각 V인 2차원 배열이 필요하니 \(O(V^2)\) 의 공간이 필요하다

모든 정점의 목록을 알아내고 싶을 때 개수와 상관없이 시간복잡도가 O(V)이다

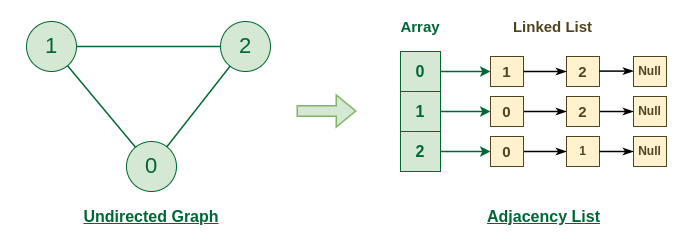
그래프와 리스트

두 번째 방법으로는 인접 리스트를 이용한다

이 방법은 정점이 많고 간선은 상대적으로 작은 상황에서 공간을 절약할 수 있는 방식

경우에 따라 인접 행렬로는 절대 저장이 불가능해 인접 리스트를 써야만 하는 상황이 있다

V개의 리스트를 만들어 각 리스트에 자신과 연결된 정점을 넣으면 된다

인접 리스트는 O(V+E)의 공간이 필요하다

인접 행렬과 인접 리스트의 시간 복잡도 비교

연산	인접 행렬 (Adjacency Matrix)	인접 리스트 (Adjacency List)
간선 존재 여부 확인 (u → v)	O(1)	O(degree(u))
정점 u의 인접 노드 순회	O(V)	O(degree(u))
간선 추가 / 삭제	O(1)	O(1)
전체 간선 순회	O(V²)	O(V + E)
메모리 사용량	O(V²)	O(V + E)

V: 정점(Node) 수

E: 간선(Edge) 수

degree(u): 정점 u에 연결된 간선 수

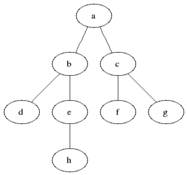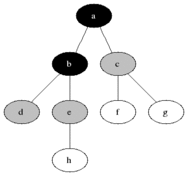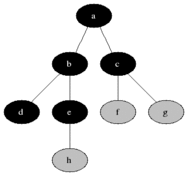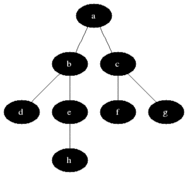
BFS (Breadth-First Search)

그래프에서 너비를 우선으로 방문하는 알고리즘

BFS

# 정렬된 graph = [[], [2, 3, 4], [1, 4], [1, 4], [1, 2, 3]]
# BFS로 출력하는 함수 (edge list -> adj list[인접 리스트] 필요)
def print_bfs(start, graph):
    visited = [False] * len(graph)
    queue = deque()
    queue.append(start)
    visited[start] = True

    while queue:
        now = queue.popleft()
        print(now, end=" ")

        for neighbor in (graph[now]): # 방문 순서를 오름차순으로 정렬
            if not visited[neighbor]:
                visited[neighbor] = True
                queue.append(neighbor)

시작 정점을 큐(Queue)에 삽입하고, 해당 정점을 방문 처리한다
큐에서 정점을 꺼내어, 그 정점과 연결된 모든 정점을 확인한다
인접 정점 중 아직 방문하지 않은 정점이 있다면,
- 해당 정점을 방문 처리하고
- 큐에 삽입한다
큐가 빌 때까지 2~3번 과정을 반복한다

BFS 활용 - 최단거리

DFS (Depth-First Search)

그래프에서 깊이를 우선으로 방문하는 알고리즘

DFS

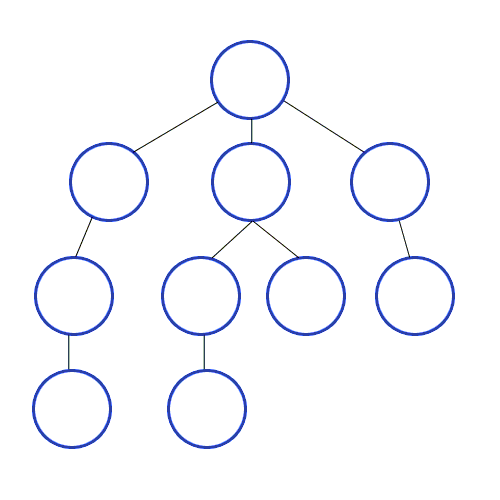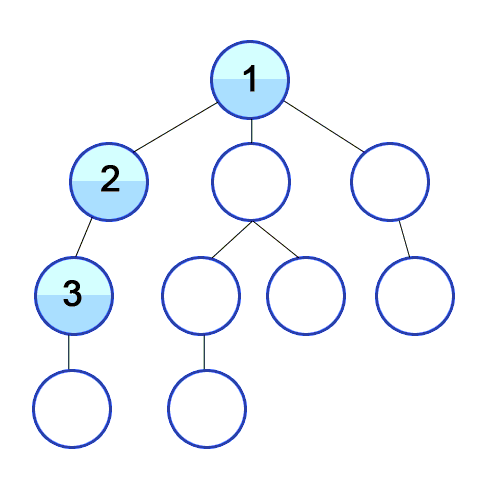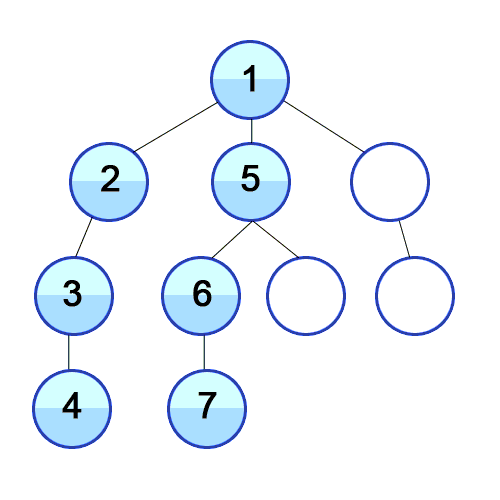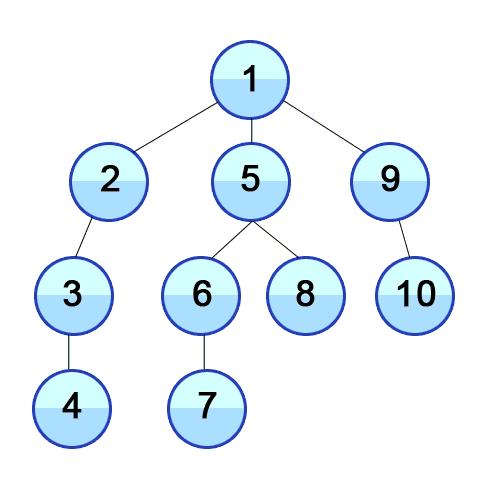
# 정렬된 graph = [[], [2, 3, 4], [1, 4], [1, 4], [1, 2, 3]]
# DFS로 출력하는 함수 (edge list -> adj list[인접 리스트] 필요)
def print_dfs(start, graph):
    visited = [False] * len(graph)
    stack = []
    
    stack.append(start)

    while stack:        
        node = stack.pop()
        if not visited[node]:
            visited[node] = True
            print(node, end=" ")
            # 이웃 노드를 오름차순으로 방문하면 역순 push
            for neighbor in reversed(graph[node]):
                if not visited[neighbor]:
                    stack.append(neighbor)

시작 정점을 방문 처리하고, 스택(Stack) 또는 재귀 함수를 이용해 탐색을 시작한다.
현재 정점에서 인접한 정점 중 방문하지 않은 정점이 있다면:
- 그 정점을 방문 처리하고
- 스택에 넣거나 재귀 호출로 다음 정점으로 이동한다.
더 이상 방문할 정점이 없다면, 이전 정점으로 되돌아가 다시 인접 정점을 탐색한다.
모든 정점을 방문할 때까지 위 과정을 반복한다.

DFS 활용 - 백트랙킹, 순열/조합 생성, 트리 후위 계산

그래프(graph)

그래프의 표현법

인접 행렬과 인접 리스트의 시간 복잡도 비교

BFS (Breadth-First Search)

DFS (Depth-First Search)

관련 알고리즘 정리