2025-07-25

해시 테이블(Hash Table)

Index

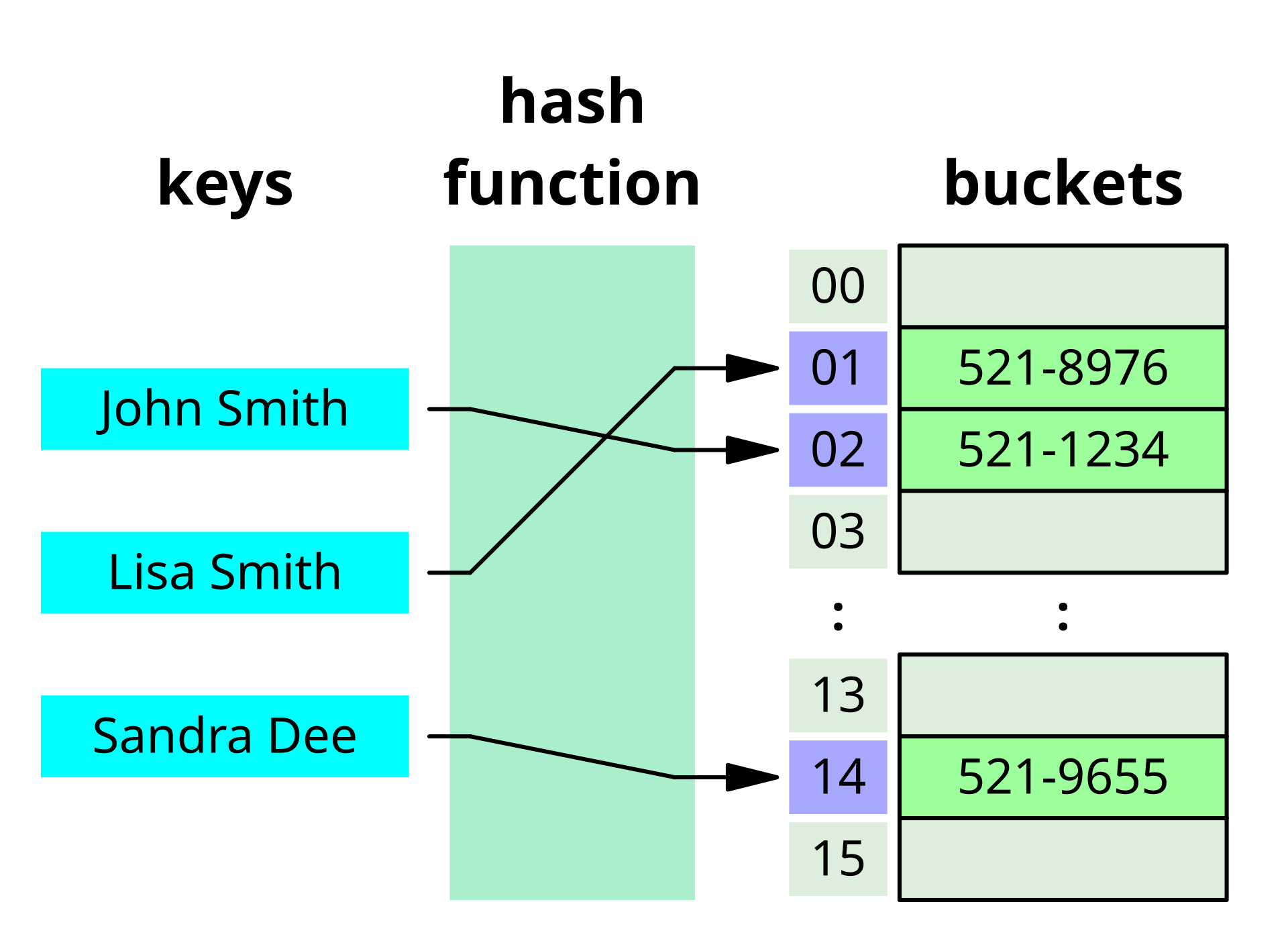
해시 테이블-1

해시 테이블은 데이터를 저장할 위치를 정하기 위하여 해시 함수(hash function)을 사용한다

해시 함수는 키(key)를 고정된 범위의 정수(배열 인덱스)로 변환하고, 이 인덱스를 통해 배열에 데이터를 저장한다

서로 다른 키가 같은 인덱스로 해시되는 경우를 해시 충돌이라고 한다

충돌은 피할 수 없기 때문에, 이를 잘 처리하는 것이 해시 테이블의 성능을 좌우한다

두 개의 충돌 처리 방법이 있다

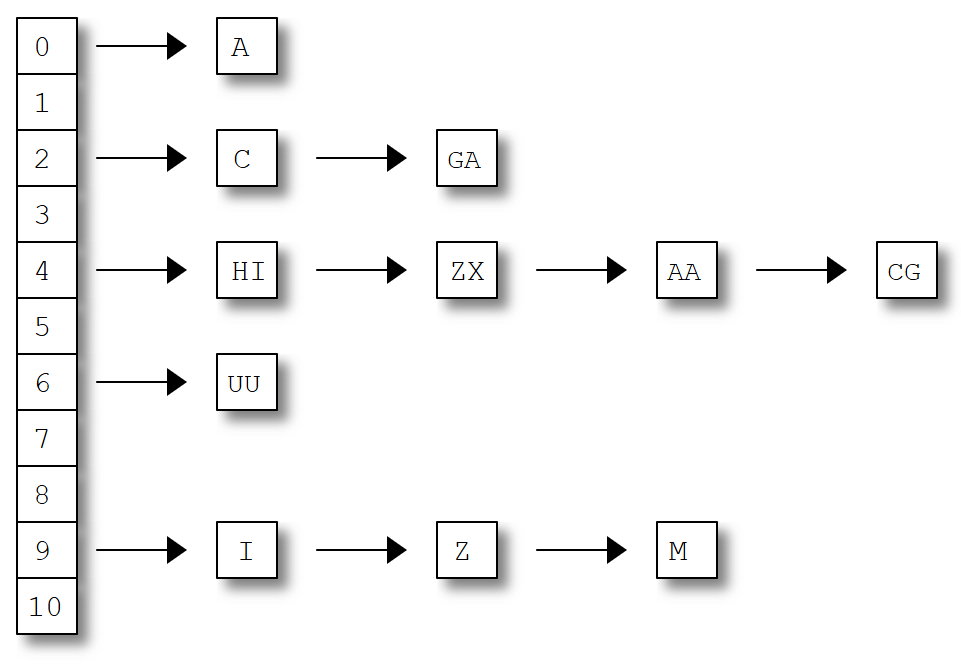
해시 테이블-2

각 인덱스마다 연결 리스트(혹은 동적 배열)을 이용하여 같은 해시값을 가진 항목들을 저장한다

충돌된 항목들을 같은 버킷 안에 저장하는 방식

최악의 경우 한 개의 해쉬 값이 다 같을때 리스트를 순회하므로 O(N) 시간 복잡도가 된다

그렇기 때문에 해시는 각 해시 값이 최대한 균등하게 퍼지는게 좋다

주어진 데이터에 대한 좋은 해시 함수를 선택해야 한다

충돌이 발생했을때 배열 내 다른 빈 인덱스를 찾아서 저장하는 방식

대표적인 방법으로는

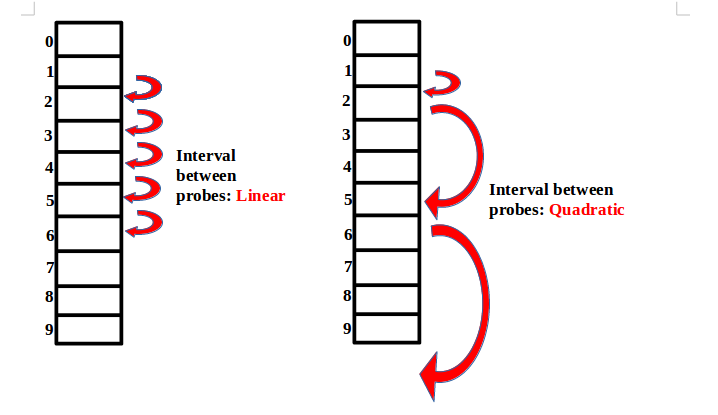
선형 탐사(Linear Probing) : 충돌 시 한칸씩 오른쪽으로 탐색, Cache hit rate가 높음, Clustering(군집) 문제가 있음
이차 탐사(Quadratic Probing) : 충돌 시 거리 제곱만큼 점프(1, 4, 9, …), Clustering에 있어서 일부분 개선
이중 해싱(Double Hashing) : 두 개의 해시 함수를 이용해 점프의 간격을 조정, Cache hit rate가 Clustering 문제를 가장 잘 해결

선형 탐사에서는 충돌 시 다음 인덱스를 검사해서 같은 값을 찾는다

하지만 삭제를 할때 그냥 빈 공간으로 두면 안되고 dummy(쓰레기 값)이나 별도의 배열을 두어서

제거된 상태임을 명시해줘야 한다

find, erase 등 탐색을 할때는 dummy 칸을 만나도 계속 탐색을 해야하고

insert를 할때는 dummy를 만나면 바로 삽입 할 수 있어야 한다

해쉬 테이블-3

해시 테이블에 저장된 요소의 개수 N과 테이블 크기 M의 비율을 부하율이라고 하며

일정 비율이 넘어가면 테이블 크기를 재할당(resize)하고, 모든 데이터를 다시 해시해야 한다

O(1) 일때

O(N) 일때