힙 정렬(Heap Sort)

 

1. 자료가 완전 이진 트리여야 한다

2. 힙은 부모의 값이 자식의 값보다도 항상 크거나 항상 작아야 한다 (heap = 쌓아 놓은 더미)

3. 힙은 노드의 형제 대소 관계가 정해져 있지 않으므로 부분 순서 트리라고도 한다

4. 아래와 같은 규칙이 성립한다

   원소 a[i]에서

   • 부모: a[(i-1) // 2]
   • 왼쪽 자식: a[i * 2 + 1]
   • 오른쪽 자식: a[i * 2 + 2]

5. 힙에서 최댓값은 루트에 위치한다는 특징을 이용하여 정렬하는 알고리즘이다

 

힙에서 최댓값인 루트를 꺼내고 루트 이외의 부분을 힙으로 만든다

이 과정에서 꺼낸 값을 나열하면 정렬이 끝난 배열이다

즉 힙 정렬은 선택 정렬을 응용한 알고리즘이다

 

코드 리뷰

출처 : 자료구조와 함께 배우는 알고리즘 입문 파이썬 편

from typing import MutableSequence

def heap_sort(a: MutableSequence) -> None:
"""힙 정렬"""

def down_heap(a: MutableSequence, left: int, right: int) -> None:
    """a[left] ~ a[right]를 힙으로 만들기"""
    temp = a[left]      # 루트

    parent = left
    while parent < (right + 1) // 2:
        cl = parent * 2 + 1     # 왼쪽 자식
        cr = cl + 1             # 오른쪽 자식
        child = cr if cr <= right and a[cr] > a[cl] else cl  # 큰 값을 선택합니다.
        if temp >= a[child]:
            break
        a[parent] = a[child]
        parent = child
    a[parent] = temp

n = len(a)

for i in range((n - 1) // 2, -1, -1):   # a[i] ~ a[n-1]을 힙으로 만들기
    down_heap(a, i, n - 1)

for i in range(n - 1, 0, -1):
    a[0], a[i] = a[i], a[0]     # 최댓값인 a[0]과 마지막 원소 a[i]를 교환
    down_heap(a, 0, i - 1)      # a[0] ~ a[i-1]을 힙으로 만들기

if __name__ == '__main__':
print('힙 정렬을 수행합니다.')
num = int(input('원소 수를 입력하세요. : '))
x = [None] * num    # 원소 수가 num인 배열을 생성

for i in range(num):
    x[i] = int(input(f'x[{i}] : '))

heap_sort(x)        # 배열 x를 힙 정렬

print('오름차순으로 정렬했습니다.')
for i in range(num):
    print(f'x[{i}] = {x[i]}')

 

 

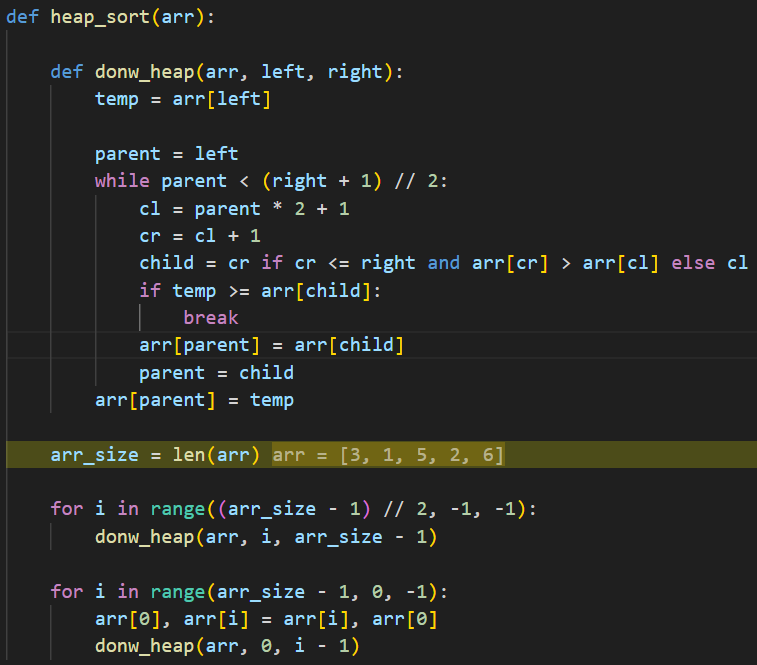
for i in range((arr_size - 1) // 2, -1, -1):
    donw_heap(arr, i, arr_size - 1)

배열의 전체를 최대 힙으로 바꾼다
(arr_size - 1) // 2는 가장 마지막 부모의 노드의 인덱스이다
역순으로(오른쪽에서 왼쪽) 훑으면서 각 부모 노드에 대해 down_heap을 수행하며 전체 배열이 최대 힙이 된다

• 왼쪽 자식 : 2*i + 1
• 오른쪽 자식 : 2*i + 2
• 부모 노드 : (i - 1) // 2

 

for i in range(arr_size - 1, 0, -1):
        arr[0], arr[i] = arr[i], arr[0]                           
        donw_heap(arr, 0, i - 1)

arr[0], arr[i] = arr[i], arr[0]는 루트와 끝을 바꾸는 부분 donw_heap(arr, 0, i - 1)는 남은 부분을 다시 힙으로 만듬

배열의 범위는 맨 뒤로 큰 값을 보냈으므로 영역에서 제외하기 위해 arr_size - 1을 한다

 

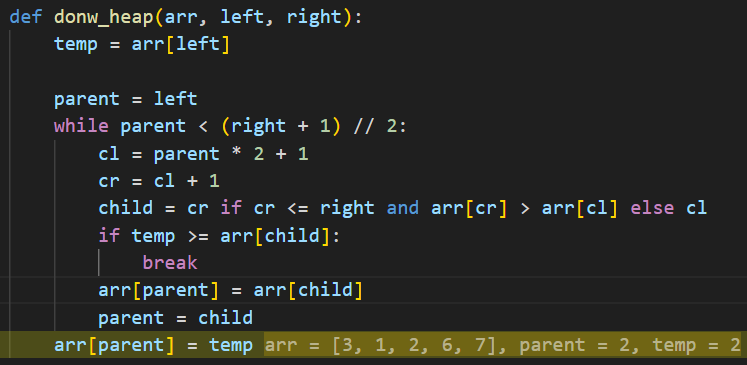
temp = arr[left]는 힙의 루트 노드를 저장한다

 

parent = left  
    while parent < (right + 1) // 2:

부모가 자식 노드를 가진 동안 계속 반복한다

 

child = cr if cr <= right and a[cr] > a[cl] else cl 

두 자식중 더 큰 값을 child로 선택한다

 

if temp >= a[child]:
    break

루트 값이 자식보다 크거나 같으면 이미 힙 조건을 만족하므로 종료

 

a[parent] = a[child]
parent = child

그렇지 않으면 자식을 부모 자리로 이동
parent = child을 하여 탐색을 한 단계 아래로 내려감

 

a[parent] = temp

더 이상 내려갈 자식이 없거나, temp가 크거나 같으면 거기서 멈추고 그 자리에 넣음

 

(n- 1) // 2 부터 0까지 내려가며 모든 부모 노드들을

down_heap으로 정리해서 배열 전체를 힙 구조로 바꾸는 것

힙 정렬의 시간 복잡도

• 힙 구성 단계 : O(N)
• 정렬 단계 (최댓값 꺼내기) : O(N log N)
• 최선 / 평균 / 최악 : O(N log N)