..

정글 알고리즘 2강

아래 내용은 경기대 배상원 교수님의 강의에서 가져왔음을 밝힙니다

Algorithms

서론

  1. 알고리즘 혼자 하기 힘든 것
  2. 재귀에 대한 이해하기

Problem and Algorithm

  1. 알고리즘은 한마디로 레시피
    • 목적하는 결과물을 만들기 위해
    • 수행해야 하는 절차, 과정을 단계별로 정확하게 기술한 것
  2. 문제와 해결방법
    • 문제가 있어야 방법을 이야기하지
    • Algorithm을 기술하기 전에 Problem을 명확히 서술 할 수 있어야 한다
  3. 수학적으로 탐구 가능한 대상
    • Problem: 가능한 입력들의 집학과 입력에 대한 출력의 쌍
    • Algorithm: 주어진 Problem에 대한 올바른 출력하게 되는 기본연산들의 Sequence(와 제어문들)
    • = 사실 함수
    • problem: 함수의 저의
    • algorithm: 해당 함수 값 계산을 하는 과정

알고리즘 기술하기

충분한 알고리즘에 대한 기술과 설명

  • What: 어떤 문제를 해결하는가
  • How: 알고리즘의 절차를 명확하게 기술
  • Why: 그렇게 수행했을 때 실제로 그 문제를 정확하게 해결함을 증명
  • How Fast: 그리고 시간이 얼마나 걸리는지에 대한 분석

자연어 기술

  • 한국어, 영어 등 자연어를 토대로 기술하여 사람이 이해하기 쉽지만 코딩하려면 더러운 작업이 필요한 경우가 많음

  • Pseudocode(슈도코드)
  • 프로그래밍 언어 코드를 닮아서 직관적이지만 특정 언어에 얽매이지 않고 자유로움

 

Program Code

  • 특정 프로그래밍 언어로 기술 혹은 구현된 알고리즘

  • (컴파일 된다는 가정하에) 가장 형식적이고 정확하지만 사람이 이해하기 어려움

  • 다른 사람의 코드를 읽는게 힘든건 당연한 것

알고리즘 분석하기

  • 주어진 혹은 직접 작성한 알고리즘 분석하는 과정
  • Correctness Proof(정확성 증명)
  • 실제로 그 알고리즘이 목적한 문제를 정확하게 해결하여 올바른 출력을 낸다는 것에 대한 증명 과정

  • 주로 수학적귀납법(Induction)을 활용

  • Running Time Analysis
  • 시간복잡도 분석
  • 그 알고리즘을 실행했을 때 시간이 얼마나 걸리는 지에 대한 분석
  • 수행되는 기본 연산의 개수 세기

 

Example:Multiplication

Multiplication Problem (곱셈 문제)

  • input: 자연수 x와 y
  • Output: x와 y의 곱 z=xy

Long Multiplication Algorithm

  • 우리가 초등학교에서 배우는 곱셈 알고리즘

  • 구구단의 시간복잡도는? n자리 n자리의 곱의 시간복잡도는 = n제곱 혹은 n제곱의 비례한다

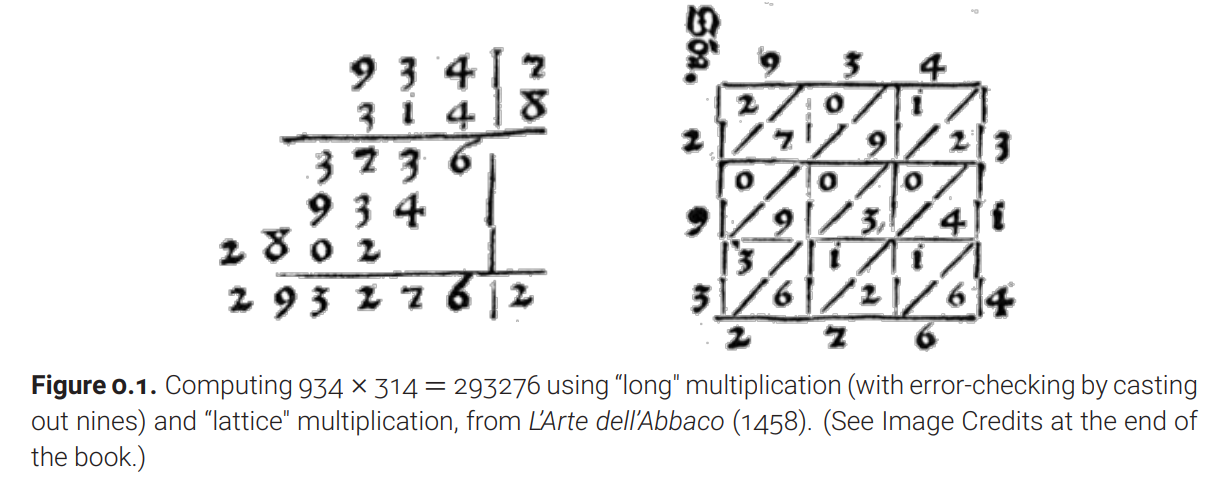
figure 0.1 Computing

 

long and lattice multiplication

  • Three Algorithms for Multiplication
  • long Multiplication
  • Lattice multiplication

이게 전부일까?

  • 하나의 문제에 대해 여러가지의 Algorithm의 가능

  • Another Example: Sorting Problem

  • 정렬

    • Selection Sort
      • n개의 수 중에서 가장 작은 수를 찾는다
      • 그 수를 맨 앞으로 이동시킨다

      • 그 뒤의 n-1개의 수에 대해 위의 작업을 반복

      • i번째 반복에서 앞의 1~i-1번째 수들은 이미 정렬된 상태를 유지
    • Insertion Sort
      • n개의 수 중에 i번째 수를 꺼내서
        • 앞의 1번째~i번째 중 올바른 위치에 삽입

      • i = 2부터 n에 대해 위의 작업을 반복

      • 반복할 때 임의의 i에 대해 1~i-1번 위치의 수들은 이미 정렬된 상태를 유지함
    • Bubble Sort
      • 바로 이웃한 수들 끼리의 교환으로 정렬
    • Mergesort and Quicksort
      • Mergesort and Quicksort
        • Divide-and-Conquer 기법으로 설계된 정렬 알고리즘

        • 제대로 이해하려면 재귀(Recursion)을 이해하셔야 합니다

        • MergeSort -시간 복잡도 O(n log n)

        • QuickSort
          • 최악의 경우 O(n**2), 평균적으로 O(n log n)
          • 대체적으로 빠르다

 

Recursion

  • 모두 재귀로 재귀한다

알고리즘 설게 기법

  • Divide-and-Conquer (분할정복)
  • Backtracking
  • Dynamic programming (동적 계획법)
  • Greedy Algorithms

트리 및 그래프 순회 알고리즘

  • In/Pre/Post-order traversal
  • DFS, BFS

반복문 - 재귀

  • 서로 변환 가능함

 

Recursive definition in mathematrics

\[n! = \begin{cases} 1 & \text{if } n = 0 \\ n \cdot (n - 1)! & \text{if } n > 0 \end{cases}\]

자연수의 정의

  • 1은 자연수이다
  • n이 자연수이면, n보다 1 큰 수도 자연수이다

 

Data Structures(자료구조)

  • (Linked)List
  • Null List

  • A가 List이면, A 앞에 노드를 연결한 전체도 List

  • Binary Tree
  • 공집합은 Binary Tree이다

  • T1과 T2가 Binary Tree라면

  • Recursive Algorithms & Recursive Functions (재귀함수)

 

Reduction

  • 알고리즘 설게에서 가장 사용하는 (거의) 유일한 기술
  • Reducing one problem X to another problem Y
  • X를 풀기 위한 알고리즘을 기술 할때 Y의 알고리즘의 이용함 -> Black Box, Subroutine

주의!

  • 활용하는 Y의 알고리즘이 어떻게 동작하는 지는 신경 쓰지 않는다
  • 단 알고리즘이 문제 Y를 정확하게 해결한다는 것만 가정한다
  • 말 그대로 Black Box처럼 생각하라

example

  • 배열 A[0..n-1]에서 최솟값 찾기
    • A를 정렬한다
    • return A[0]
  • Selection(A[0..n-1],k) // 배열 A에서 k번째로 작은 값 찾기
    • A를 정렬한다
    • return A[k-1]
  • Selection문제를 정렬 문제로 Reduce하여 해결

 

사실 우리들이 항상 사용하고 있는 기술

  • 복잡한 문제를 해결하기 위해 단계를 나누는 것
    • 각 단계는 더 단수화된 문제를 해결
  • 내가 작성하는 함수에서 다른 함수를 호출하는 것
    • 내가 만든 다른 함수
    • 남이 만든 함수, Library Functions, Methods (STL, Packages)
    • 기본 연산자

 

알고리즘을 설계할 때(함수를 작성할 때)

  • 사용하는 Basic Building Block들이 어떻게 동작하는 지 몰라도 됨

  • 내 알고리즘(내 함수)이 다른 알고리즘(혹은 함수)에서 building block으로써 사용될 수 있을지 몰라도 됨

  • 내부 동작 방식을 이해하고 있어도 모르는척 무시하는 것이 더 도움이 됨

  • 초보자들은 불편하게 생각되지만, 전문가에게는 자연스러워

  • 함수위에 주석을 꼭 달아라

 

Recursion

Recursion은 특별한 종류의 reduction!

  • 주어진 문제의 instance가 충분히 작아서 바로 풀 수 있으면, 바로 풀어
  • 그렇지 않으면 , 같은 문제의 더 작은 Instance(Subproblem)로 Reduction 한다

 

Hanoi Tower

  • n개의 Disc와 3개의 Peg (말뚝)

규칙

  • 한 번에 하나의 disc를 원래의 peg에서 다른 peg을 옮긴다(move 연산)
  • 큰 disc가 작은 disc위에 올라가서는 안된다

Hanoi Tower 문제

  • n개의 disc를 peg 1에서 peg 3으로 옮기는 방법

  • 몇 번의 move 연산이 필요한가

  • n개의 disc를 Peg 1에서 Peg 3로 옮기기
  • n-1개의 disc를 Peg 1에서 Peg 2로 옮긴다 (by recursion)
  • Disc n을 Peg 1에서 Peg 3로 이동(Move)
  • n-1개의 disc를 Peg 2에서 Peg 3로 옮긴다 (by recursion)

 

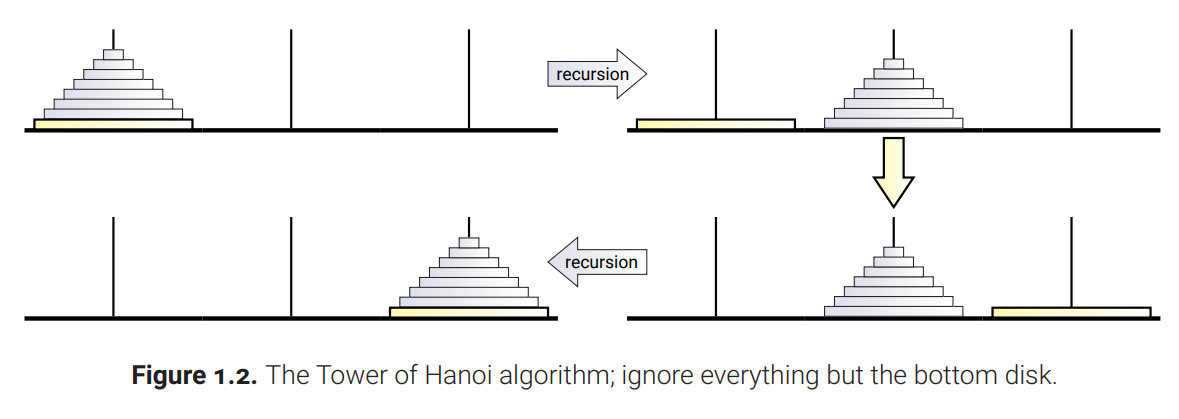
figure 1.2 the tower of hanoi algorithm

  • n-1개를 옭기는 것은
    • 원래 instance보다 작은 Hanoi tower문제의 instance -> subproblem
    • 같은 문제로의 reduction -> recursion
  • Hanoi(n, src, dst, temp)
    • n개의 disc를 Peg src에서 Peg dst로 Peg tmp를 이용하여 옮기기

 

Recursion은 Reduction의 일종

  • Base Case
  • Recursion Step

Simplify & Delegate

  • Simplify : 더 작은 Instance(Subproblem)을 만들고
  • Delegate : 던져버리고 잊어버려(Recursion의 magic, recursion fairy - 내 뒤의 재귀 요정에게 부탁)

Hanoi Tower: 시간 복잡도 분석

  • Move 연산을 몇번 수행하게 될까
  • T(n)을 Hanoi(n, src, dst, tmp) 함수를 실행했을 때 Move 연산 수행 횟수라고 정의 하자

 

\[T(n) = \begin{cases} 0 & \text{if } n = 0 \\ 2 \cdot T(n - 1) + 1 & \text{if } n > 0 \end{cases}\]

Mergesort

  • Recursion을 이용하여 정렬 알고리즘
    • 1945 John von Neumann에 의해 개발되어
    • EDVAC에 구현된 최초의 컴퓨터 프로그램 중 하나

 

Mergesort의 방법

  1. 주어진 배열(대략 절반으로) 둘로 나눈다
  2. 두 subarray를 각각 정렬한다
  3. 정렬된 두 subarray를 합쳐서(merge) 하나의 정렬된 배열로 만든다

Time Complexity

  • T(n)의 점화식
\[T(n) = \begin{cases} \Theta(1) & \text{if } n = 1 \\ T\left(\left\lfloor \frac{n}{2} \right\rfloor\right) + T\left(\left\lceil \frac{n}{2} \right\rceil\right) + \Theta(n) & \text{if } n > 1 \end{cases}\]

이 점화식을 풀면 T(n) = O(nlogn)