위상 정렬(Topological Sort)
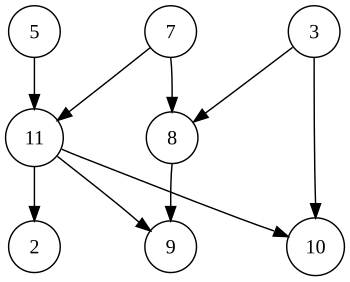
위상 정렬은 사이클이 없는 방향 그래프(Directed Acyclic Graph)에서 정점들의 선후 관계(의존성)를 지켜 순서를 정렬하는 알고리즘
진입 차수 0인 노드 없다는 건 사이클이 존재한다는 뜻
사이클이란 방향 그래프에서 어떤 정점으로부터 시작해 다시 자기 자신으로 돌아오는 경로가 존재하는 경우를 말한다
사이클이 생기면 “A를 하려면 B가 먼저여야 하고, B를 하려면 C가 먼저여야 하며, C를 하려면 A가 먼저여야 함” 같은 모순된 순서가 생겨 정렬이 불가능함
사이클 없는 방향 그래프에서 위상 정렬이 가능하다
들어오는 간선이 없는 정점을 제거하는 방식으로 위상 정렬을 구현할 수 있다
-
그래프의 모든 간선을 순회하여, 각 정점의 진입 차수(indegree)를 계산함
-
indegree가 0인 정점들을 모두 큐에 넣음
-
큐에서 정점을 꺼내어 위상 정렬 결과에 추가한다
-
꺼낸 정점과 연결된 모든 정점의 indegree 값을 1 감소한다
-
이 때 indegree가 0이 되었다면 그 정점을 큐에 추가한다
-
큐가 빌 때까지 3, 4번 과정을 반복한다
-
indegree 0인 정점이 여러 개면 순서가 달라질 수 있음
-
결과에 포함된 노드 수 < 전체 노드 수 → 사이클 존재
-
사이클을 이루는 노드들은 서로를 의존하고 있음
-
따라서 indegree가 절대로 0이 되지 않음
-
코드 리뷰
from collections import deque, defaultdict
# 1. 그래프 초기화
V = 6 # 과목 수
graph = defaultdict(list)
indegree = [0] * (V + 1) # 1번부터 6번까지 사용
# 2. 간선 정보 추가 (선수 과목 → 후속 과목)
edges = [
(1, 2), # 자료구조 → 알고리즘
(3, 2), # 계산론 → 알고리즘
(2, 6), # 알고리즘 → 컴파일러
(1, 4), # 자료구조 → 컴퓨터구조
(4, 5), # 컴퓨터구조 → 운영체제
]
for a, b in edges:
graph[a].append(b)
indegree[b] += 1
# 3. 위상 정렬 함수
def topological_sort():
result = []
q = deque()
# 진입 차수 0인 노드부터 시작
for i in range(1, V + 1):
if indegree[i] == 0:
q.append(i)
while q:
cur = q.popleft()
result.append(cur)
for nxt in graph[cur]:
indegree[nxt] -= 1
if indegree[nxt] == 0:
q.append(nxt)
if len(result) != V:
print("사이클이 존재하여 위상 정렬 불가능")
else:
print("위상 정렬 결과:", result)
topological_sort()
위상 정렬 결과: [1, 3, 2, 4, 5, 6]
-
1 (자료구조): 가장 먼저 가능 (선수 과목 없음)
-
3 (계산론): 역시 선행 조건 없음
-
2 (알고리즘): 자료구조(1), 계산론(3) 이후 가능 → OK
-
4 (컴퓨터구조): 자료구조(1) 이후 가능 → OK
-
5 (운영체제): 컴퓨터구조(4) 이후 가능 → OK
-
6 (컴파일러): 알고리즘(2) 이후 가능 → OK
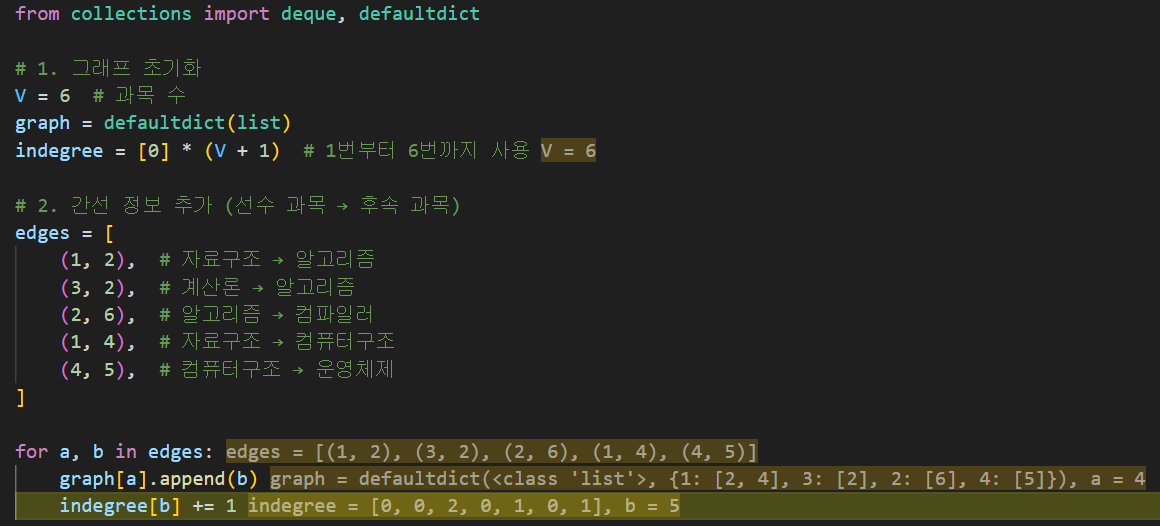
배열 : graph, indegree, edges, q, result
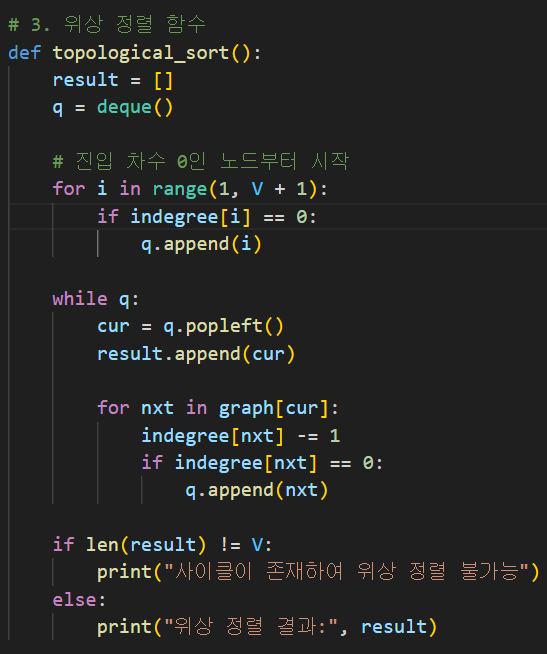
q는 진입 차수가 0인 노드 배열
cur은 큐의 앞에서 노드 하나(cur) 꺼냄 (선행 조건이 모두 충족된 상태)
꺼낸 노드들을 result에 넣는다 (위상 정렬 결과 순서에 포함)
현재(cur)에 영향을 미치는 nxt를 순회하며 indegree(진입 차수)를 감소한다
nxt의 진입 차수가 0이 되었다는건
모든 선행 노드들이 처리된 상태라는 것
큐에 넣어 다음에 처리하도록 한다
시간 복잡도
정점 수 : V, 간선 수 : E
O(V + E)